Previously, I covered discrete-time filters. Matlab has functions for continuous-time filters as well. The transform of interest is the Laplace transform. As before, we obtain a transfer function, this time in the s-domain. We have the numerator B(s) and denominator A(s) in descending powers of s. It is common, but not necessary, to normalize the leading term of A to 1. Suppose
B=[5];A=[1,2,3];
Through basic algebra, we have the partial fraction expansion
Matlab can calculate the partial fraction expansion of this function with the residue command. The output vectors r,p,k contain the residues (r terms above), poles (p terms), and the direct term k, which is not present in this function.
[r,p,k]=residue(B,A);
r =
0 - 1.7678i
0 + 1.7678i
p =
-1.0000 + 1.4142i
-1.0000 - 1.4142i
k =
[]
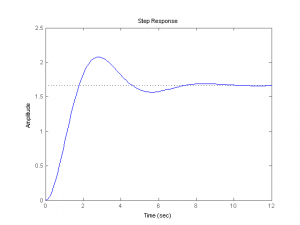
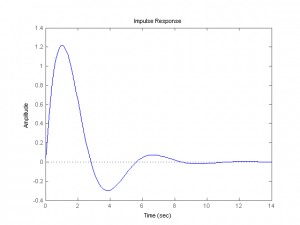
Often we’ll want to graph the impulse or step response of a filter. To have Matlab do it, we need to box it up into a transfer function object using the tf command on B and A, and then use the intuitively-named impulse or step commands. In passing, it can be noted that since the Laplace transform of the unit step is just 1/s vs. 1 for the impulse, that the step response is just the impulse response with A multiplied by s (i.e. with a trailing zero).
figure; step(tf(B,A)) figure; impulse(tf(B,A))
The resulting plots are shown below.
More generally, we can graph the response of an arbitrary linear function u(t) on the time interval [0,T] with the lsim command. Define vector u on a time interval t (in the time domain), and the lsim command graphs the response. Note the similarity between the lsim response and the step response above.
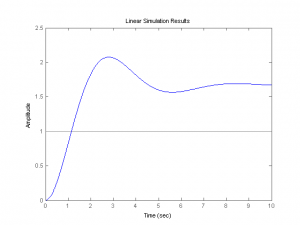
t=linspace(0,10,10000); u=ones(1,length(t)); figure; lsim(tf(B,A),u,t)
We can get the poles and zeros from the transfer function object with the pole() and zero() command. If we are performing multiple operations with the object, it’s worthwhile to create another variable for it.
H=tf(B,A); pole(H) ans = -1.0000 + 1.4142i -1.0000 - 1.4142i zero(H) ans = Empty matrix: 0-by-1